第六章 数据库E-R关系模型设计

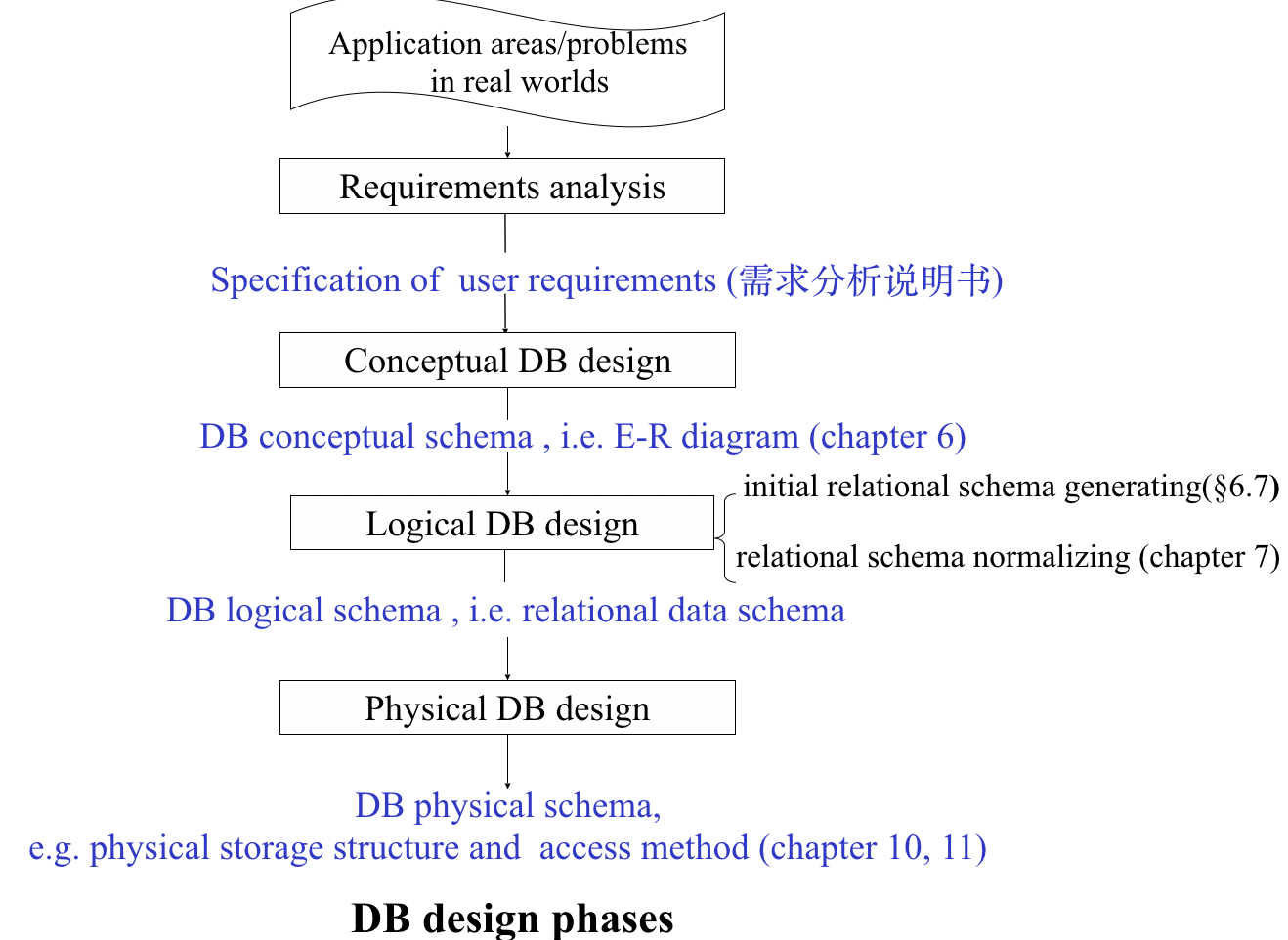
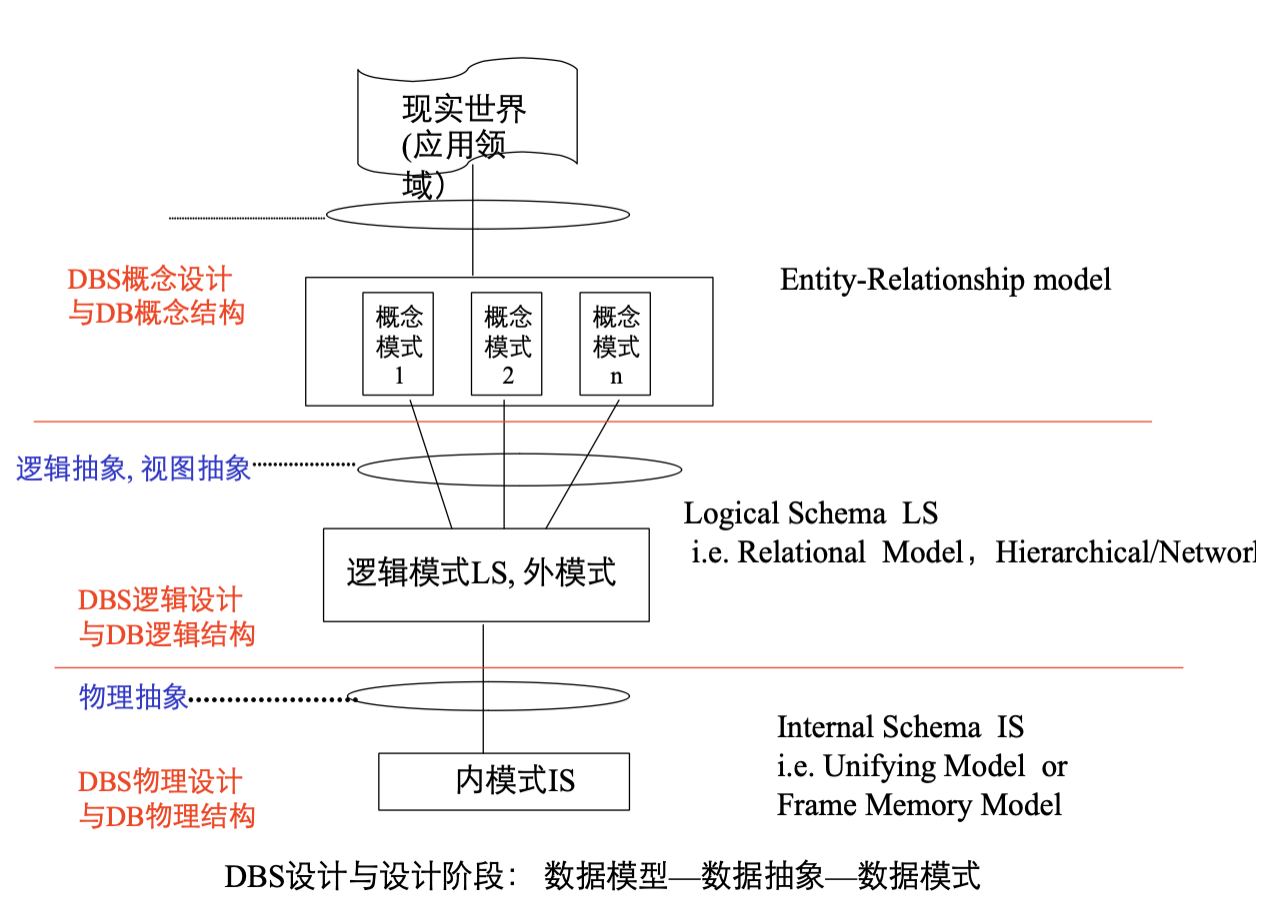
image-20231031130649955 image-20231031131454091

E-R 模型

  • entity sets 实体集
  • relations sets 联系集
  • attributes 属性

实体集 entity sets

有特性的对象称为实体

实体集 - 有相同特性的实体的集合

实体集和实体往往都用实体称呼，需要分辨

能唯一在实体集中定位一个实体的属性集合称为他的主键 primary key

没有主键的实体集称为弱实体集 weak entity sets

使用部分键（鉴别器） discriminator 作为一个弱实体的额外属性，作为辨别依据

联系集 relations sets

实体集之间在语义上的关系就是一个relation（关系/联系）

联系集就是实体集之间的语义关系集

联系集也可能有属性

degree 度

联系集的度

n元联系集表达的是联系集建立在n个实体集上，这个n就是度

Mapping Cardinality Constraints 映射基数

某实体A中的一个实体通过联系集R能同时与另一个实体集B中相联系的实体数目，取最大值

  • 一对一
  • 一对多
  • 多对一
  • 多对多

属性 attributes

根据需求，可以确定属性

属性有以下类型

  • simple 简单属性

  • composite 复合属性，可以再细分

  • single-valued 单值属性

  • multivalued 多值属性，对一个实体的取值可以有多个值，比如一个人有多个电话号码

  • derived 导出属性 可以通过其他属性计算得出的属性

    • 节约计算效率
    • 增大存储空间
    • 需要确保导出属性与被计算的属性的关系一致性

域 domain

数据的取值域

E-R模型图

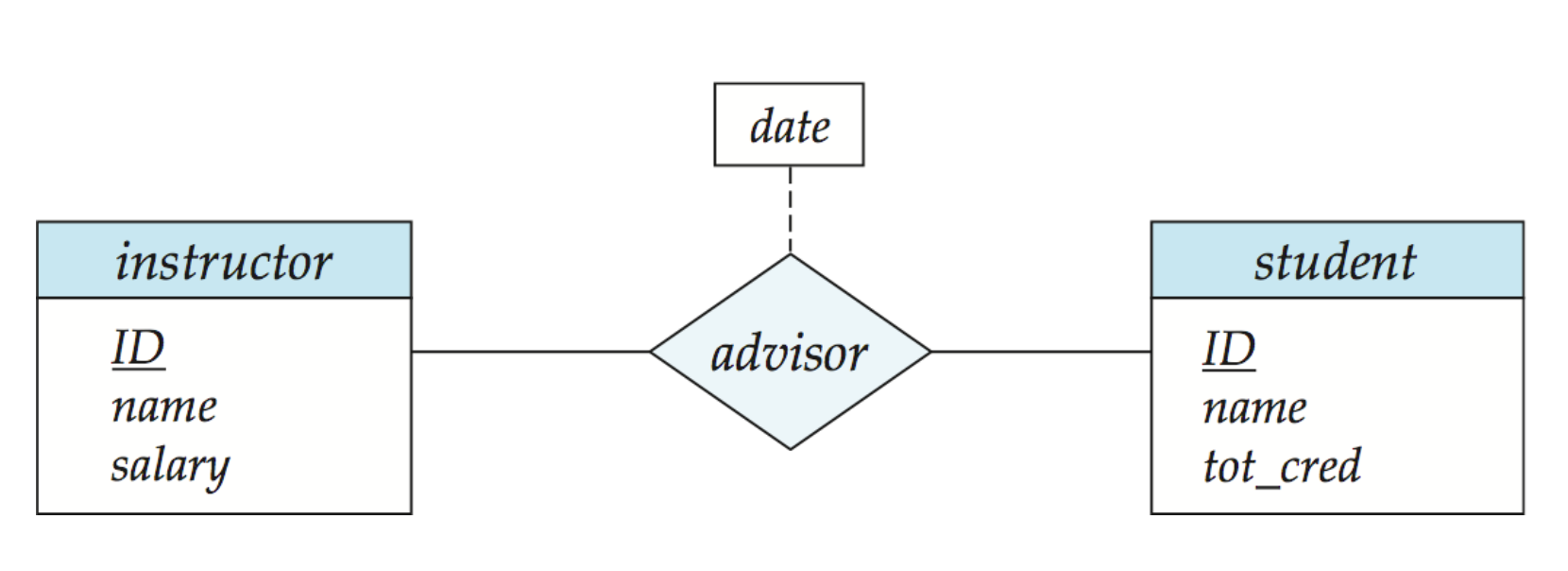
image-20231031141549871

虚线代表建立在联系集上的属性

角色 role

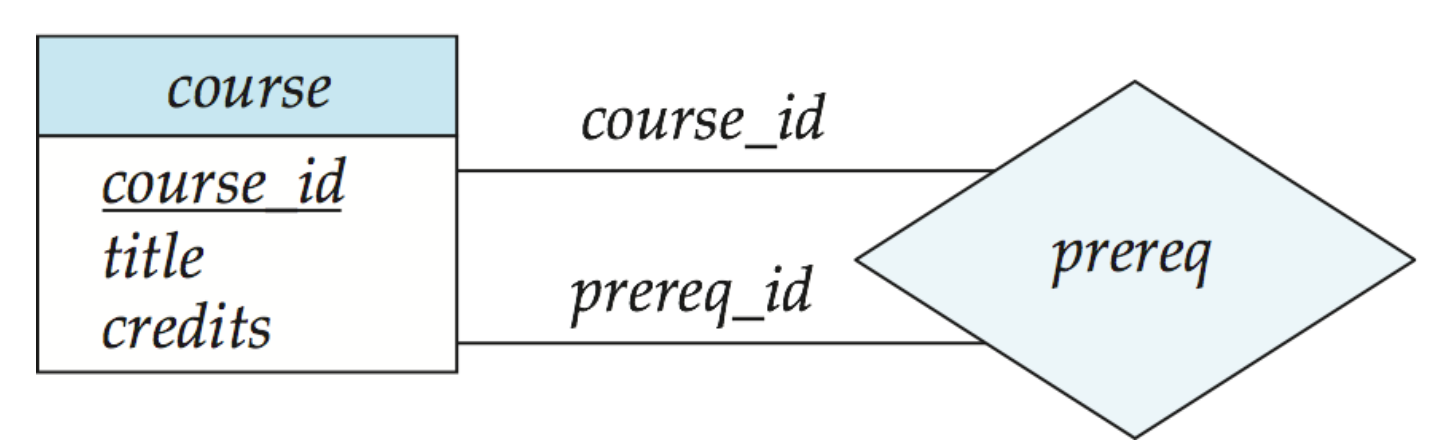
image-20231031141632883

针对一元联系，可以让每个实体集扮演一个角色

比如图中的course_id和prereq_id，都扮演了角色

映射

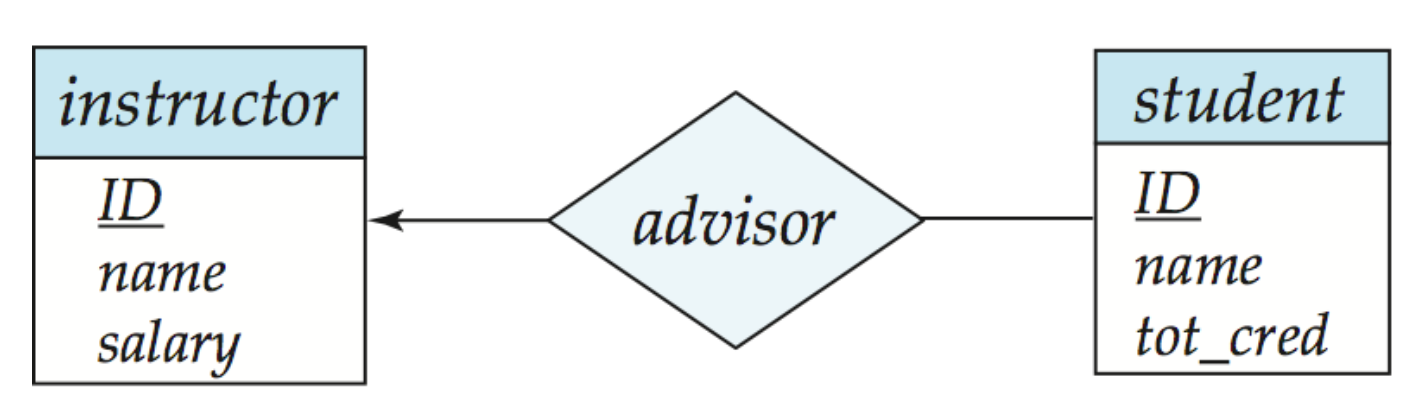
image-20231031141929598

箭头表示一，横线表示多，如图中表示一对多

全参与&部分参与 Total and Partial Participation

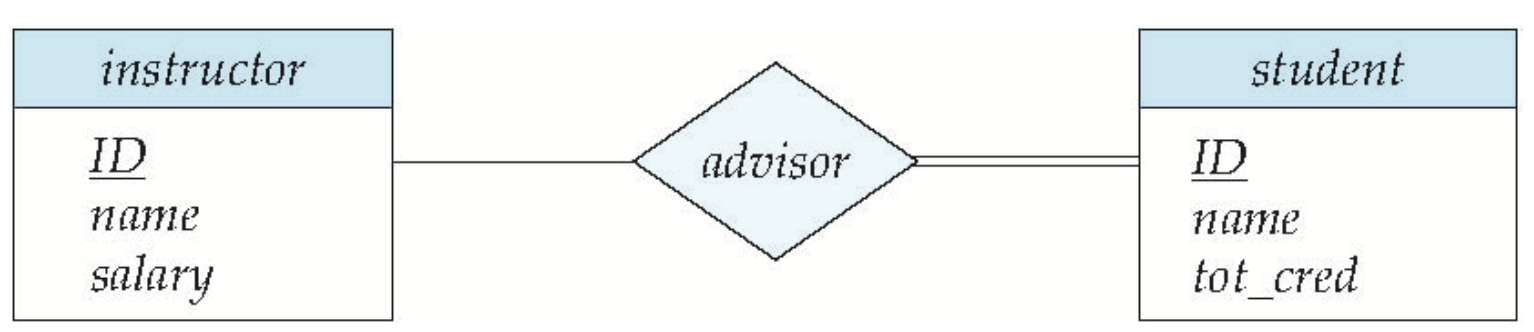
image-20231031142107848

一条横线表示实体集中部分实体参与关系

两条表示全参与

参与的标记

可以在横线上做标记<min,max>表示最小的参与和最大的参与数

  • min为1，表示全参与（每个实体至少有一个关系）

  • max为1，表示每个实体最多有一个关系

  • max为*，表示无限制

  • 一对一，则（1:1）

  • 一对多，则（1:>=2）

  • 多对多，则（*：*）

image-20231224213817081

如上图，左侧的0…*表示一个instrutor可以有最少0个，最多无限制的student，右边的1…1表示一个student可以最少最多可以有1个instructor。

也就是说，instructor -> student的关系advisor是一个一对多关系

特别注意：与正常逻辑不同，数字在哪边，反而是代表另一边的参与量！！

属性的表示

image-20231031143132121

弱联系

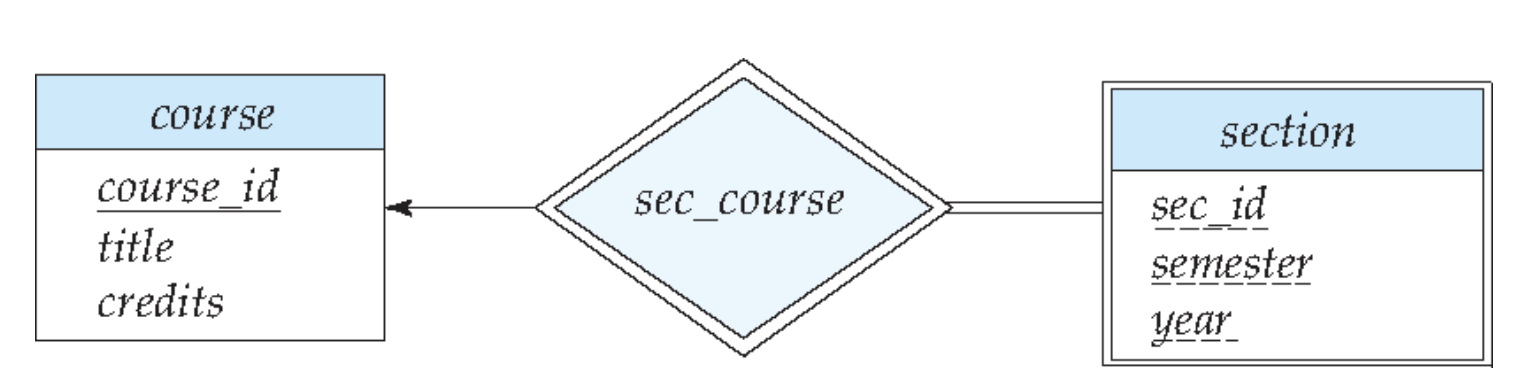
image-20231031143208525

下划虚线表示部分键

E-R模型图的建立

  1. 定义实体集
  2. 定义联系集
  3. 定义每个实体集的属性，联系集的属性
  4. 制图

E-R模型扩展：特化 Specialization

从高层实体集生成低层实体集，存在属性继承关系

正交 disjoint

一个高层实体只属于一个低层实体集

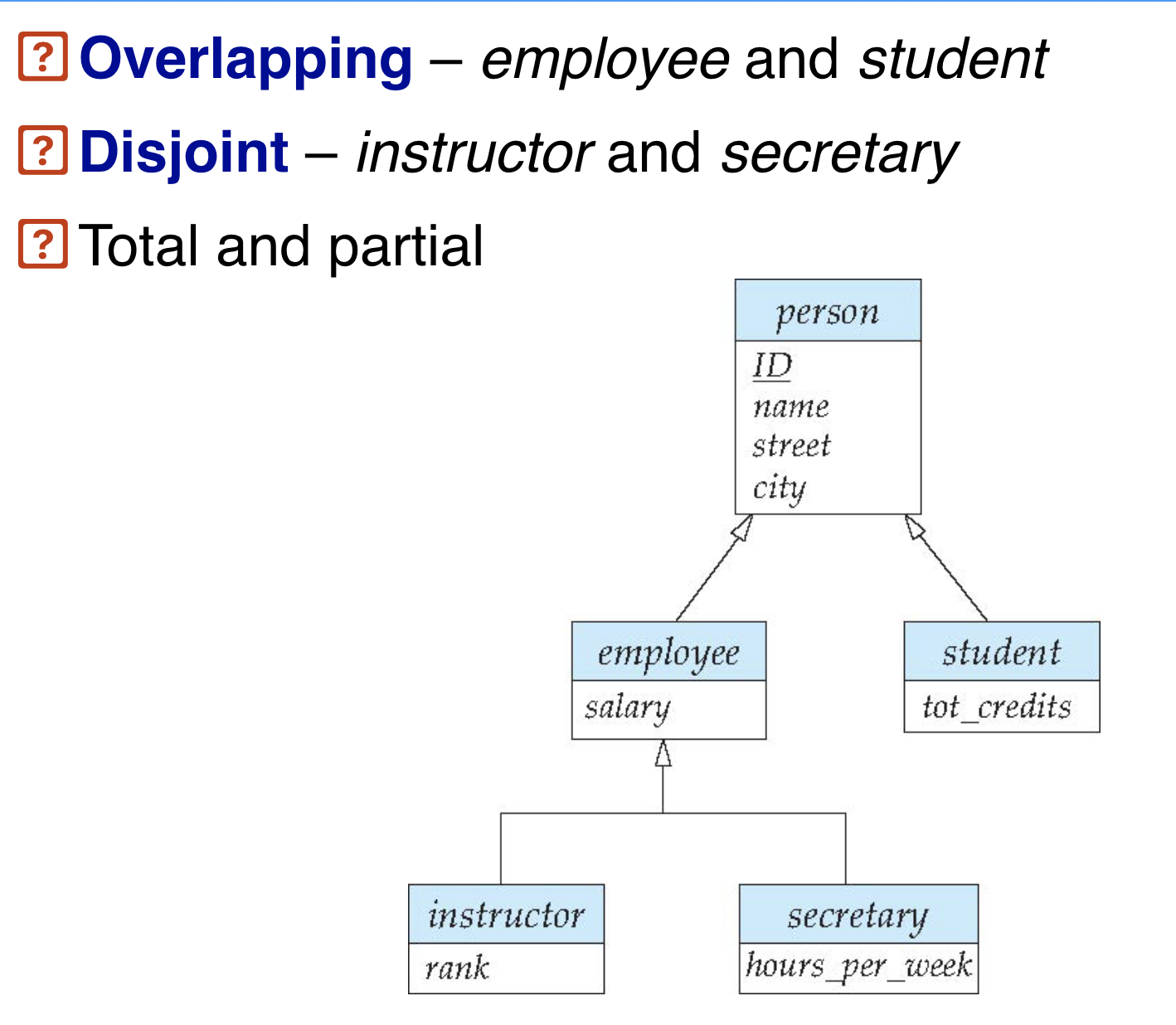
重叠 Overlapping

一个高层实体可以属于多个低层实体集

完全演绎/刻画 total specialization/Generalization

每一个高层实体至少在低层实体集出现一次

其实就是高层实体集等于低层实体集的并集

部分演绎/刻画 partial specialization/generalization

部分高层实体在低层实体集没有出现

其实就是高层实体集大于低层实体集的并集

泛化 Generalization

从低层实体集生成高层实体集（取公共实体）

特化和泛化的过程不一样，但结果E-R相同

所以有以下分类

  • 正交，完全特化/泛化
  • 正交，部分特化/泛化
  • 重叠，完全特化/泛化
  • 重叠，部分特化/泛化
image-20231107130823205

聚集 Aggregation

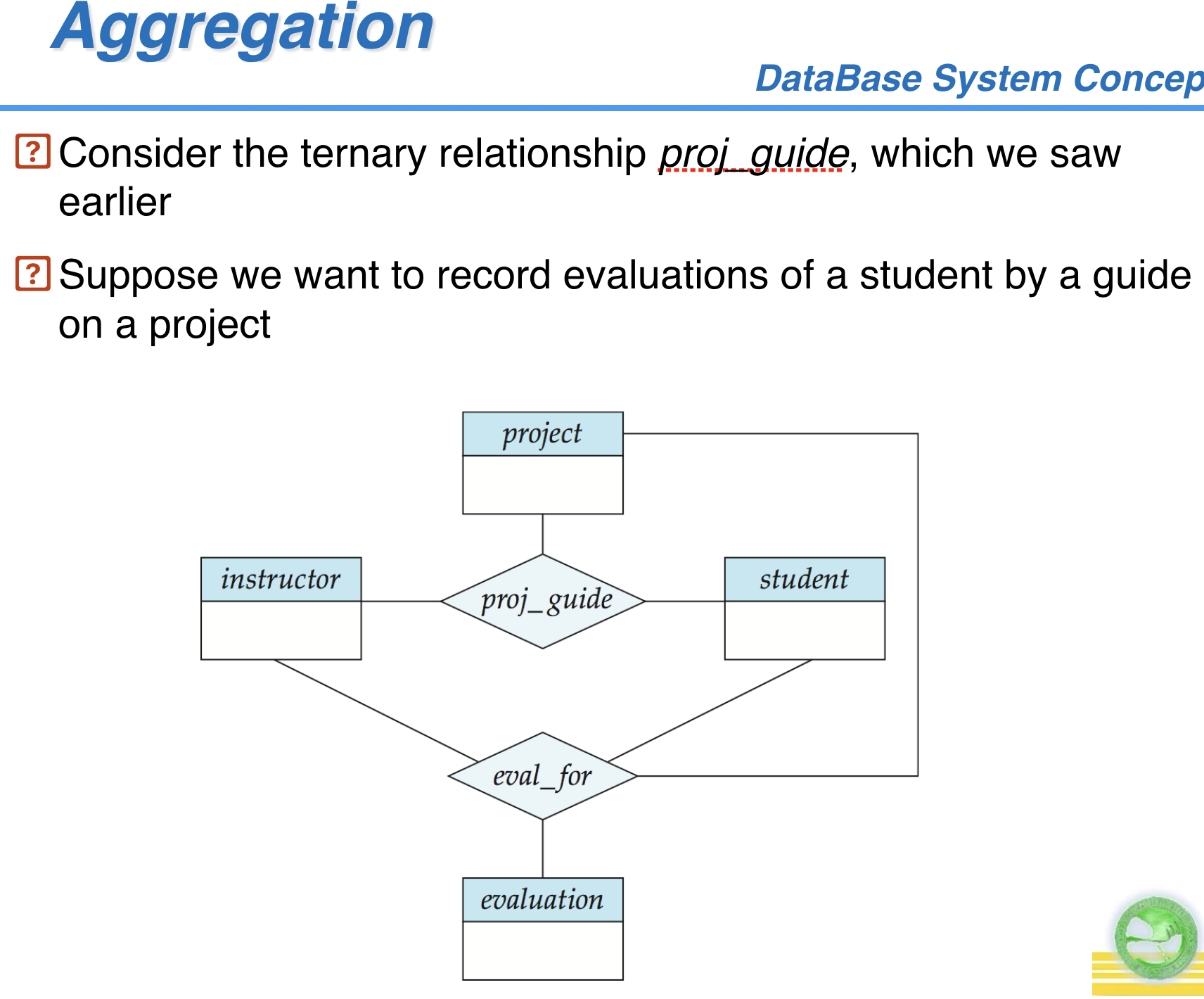
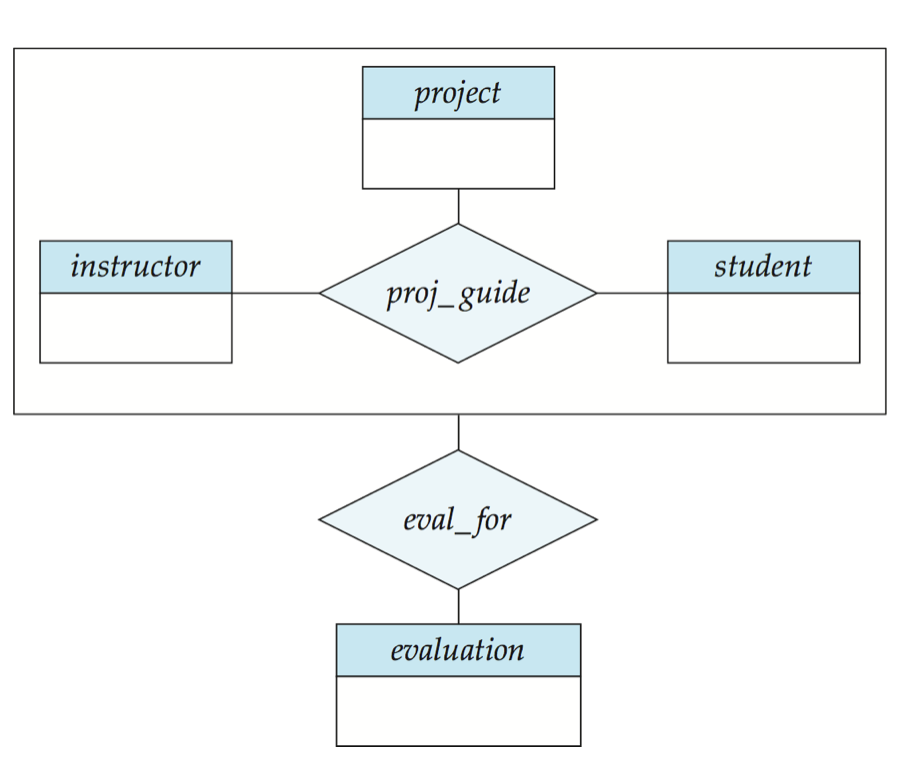
image-20231107130908896 image-20231107130955110

E-R模型的一些探讨

可以视情况定义同一概念为属性或实体

可以视情况定义同一概念为联系集或实体

非二元联系集转换为二元联系集

image-20231107132001797

E-R模型到表的转换

强实体集

  • 实体集名 - 表名

  • 实体集的主键 - 表的主键

  • 实体集的简单属性 - 表的属性

  • 实体集的复合属性 - 表中只记录复合属性的叶子节点

  • 实体集的导出属性 - 理论上表不需要，实际上要具体情况具体分析

  • 实体集的多值属性 - 为这个多值属性另外构建一张表，另外这张表包括这个多值属性作为属性，还需要包括实体集的主键作为属性，然后以这两个属性共同作为主键

弱实体集

  • 弱实体集的部分键+弱实体集关联的强实体集的主键 - 表的属性
  • 弱实体集的部分键+弱实体集关联的强实体集的主键 - 表的主键
  • 弱实体集的多值属性 - 为这个多值属性另外构建一张表，另外这张表包括这个多值属性作为属性，还需要弱实体集的全部部分键作为属性，还需要包括关联的强实体集的主键作为属性，然后以这些属性共同作为主键

联系集

  • 联系集关联的多个实体集的主键 + 联系集的属性 - 表的属性
  • 联系集关联的多个实体集的主键 - 共同作为表的主键
  • 如果联系集的属性有多值属性，要为这个多值属性另外生成一张表
  • 对于多对一的情况，通常把一的实体集的主键作为多的实体集的表的外键（不需要从联系集建一张表），这就是归并联系
  • 对于一对一的情况，可以选择其中一个“一”作为“多”的角色
  • 对上述两种情况，如果联系集上有属性，那就把属性和“一”的主键一起放到“多”建立的表作为外键

高层实体集和低层实体集

  • 高层实体集直接建表，低层实体集建表属性为高层实体集的主键和自己的属性
  • 或者只建一张表，包含高层所有属性和低层特有的属性，另外建立一个属性标识是哪个低层属性集提供属性

第7章 关系数据库设计 - 函数依赖

函数依赖 functional dependencies

  • Let R be a relation schema

​ α ⊆ R and β ⊆ R

  • The functional dependency

​ α → β

设R（U）是属性集U上的关系模式，X,Y是属性集U的子集。若对于R（U）的任意一个可能的关系r，r不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称X函数确定Y或Y函数依赖于X，记作X->Y。

holds on R if and only if for any legal relations r®, whenever any two tuples t1 and t2 of r agree on the attributes α, they also agree on the attributes β*.* That is,

​ t1[α] = t2 [α] ⇒ t1[β] = t2 [β]

就是说，如果对关系模式R的任意合法关系实例r（R），在任意时刻对一个属性a的任意两个元组t1、t2，对另一个属性b结果相同，那么可以说a确定b或者b依赖a

也就是说对a，有唯一对应一个b

一个身份证号码可以确定一个人的姓名，不存在说身份证号相同，但是是不同的人的情况。（可以做强制性规定一些条件使有的函数依赖成立。比如规定不允许同名人出现，因而使姓名->年龄）

key

  • K is a superkey（超键） for relation schema R if and only if K → R

  • K is a candidate key（候选键） for R if and only if

    • K → R

    • for no α ⊂ K, α → R 最小性（K的真子集无法推出R）

平凡依赖 trivial dependency

  • A functional dependency is trivial if it is satisfied by all instances of a relation
  • 若X->Y，且Y是X的子集（对任一关系模式，平凡函数依赖必然成立），就是平凡函数依赖。

E.g.

ID, name → ID*

name → name

In general, α → β is trivial if β ⊆ α

在学生表(学号,姓名,年级)中,(学号,姓名)可以推出学号和姓名其中的任何一个,这就是平凡函数依赖.

直白点说，就是只要Y是X的子集，Y就依赖于X

传递依赖 Transitive dependency

  • 如果一个函数依赖有以下关系

    α→β，（β⊈α），β↛α，β→γ，α → β ，（ β\nsubseteq α ）， β\not \to α ， β \to γ ，

    那么γ\gamma是α\alpha的传递依赖

    • β↛αβ\not \to α的限制是因为如果β→αβ \to α，那么α→γ\alpha \to \gamma会变成直接依赖

部分依赖 partial dependency

  • 如果一个函数依赖有以下关系

α→β,γ⊂α,γ→βα → β , γ ⊂α, γ → β

​ β 是 α 的部分依赖

比如（学号，姓名）确定性别，但是实际上学号就能确定性别

逻辑蕴含 logically imply

设F是在关系模式R上成立的函数依赖的集合，X→Y是一个函数依赖。 如果对于R的每个满足F的关系r也满足X→Y，那么称F逻辑蕴含X→Y

Closure of a Set of Functional Dependencies 函数依赖集闭包

用F+表示F的闭包

  • For R(U,F), The set of all functional dependencies logically implied by F is the closure of F.

    • E.g. If F={A → B ,B → C}, then F+ = {A→A,A→B,B→C,B→B,A→C}
三个定律
  • reflexivity (自反律）: if β ⊆ α, then α → β
  • Augmentation（增广律）: if α → β*,* then γ α → γ β
  • transitivity （传递律）: if α → β*,* and β → γ, then α → γ

union 合并律

If α → β holds and α → γ holds, then α → β γ holds

(α → β , α → α β ; α → γ, α β → β γ; α → β γ )

Decomposition 分解律

If α → β γ holds, then α → β holds and α → γ holds

(α → β γ , β γ → β , α → β )

pseudotransitivity 伪传递律

If α → β holds and βγ → δ holds, then α γ → δ holds

(α → β , α γ → βγ ; β γ→ δ , α γ → δ )

Closure of Attribute Sets 属性集闭包

α+是F下的属性集闭包\alpha^+是F下的属性集闭包

α→β is in F+➳β⊆α+α → β\ is\ in\ F^+ ➳ β ⊆ α^+

1
2
3
4
5
6
7
8
9
10
Input: α , F
Output: α+

result := α;
while (changes to result) do
	for each β → γ in F do
		begin
			if β ⊆ result then
				result := result ∪ γ 
		end

如果a是一个超键，那么a+包含R的所有属性

如果a->b的函数依赖成立，只用满足b在a+中

求F的闭包，对R中的每个y（y是子集，记住属性可以组合），找到y+，对每个闭包构成的函数依赖关系就是F的函数依赖集闭包

属性集闭包的作用

  • 测试属性A是否为超键

    计算A+A^+，判断它有没有包含R中全部属性

  • 测试函数依赖

    如果要判断一个函数依赖α→β\alpha \to \beta是否被F逻辑蕴含，可以通过计算α+\alpha^+是否包含β\beta来判断

  • 计算F的函数依赖集闭包

    对每个γ∈R\gamma \in R，计算其闭包γ+\gamma^+，对每个属性S∈γ+S\in \gamma^+，可以得到函数依赖γ→S\gamma \to S

如果两个函数依赖集闭包 F+ = G+，认为F与G等价

F+ = G+ ⇔ F⊆G+，G⊆F+

(F+⊆G+，G+⊆F+ )

最小覆盖/正则覆盖/最小函数依赖集Canonical Cover/Minimal Cover

与F+等价的函数依赖集可能有很多个，但这里我们需要F的最精简的函数依赖集，不包含无关属性（求闭包去掉），且式子左边是独一无二的（如果有相同的用合并律合并）

  • Fmin 等价于 F
  • Fmin的每个函数依赖右部没有冗余属性
  • Fmin中没有冗余的函数依赖
  • Fmin的每个函数依赖左部没有冗余属性

{A → B, B → C, A → C} 最精简就是 {A → B, B → C}

最小覆盖可能不唯一，但他们都等价

可以采取以下手段：

  • 先将每个函数依赖右部分开为单属性
  • 去除左部冗余属性（无关属性）
  • 去除冗余的函数依赖（对A→BA\to B,如果去掉这条式子后B∈A+B\in A^+，就可以去掉）
  • 合并相同左部

eg

关系模式r(A,B,C,D,E)的函数依赖集F:
A->BC
CD->E
B->D
E->A

  • 右部分化为单属性后,
    A->B
    A->C
    CD->E
    B->D
    E->A
  • 去掉左边冗余属性
    A->B
    A->C
    CD->E
    B->D
    E->A
  • 去掉冗余函数依赖
    A->B
    A->C
    CD->E
    B->D
    E->A
  • 合并,得最终结果
    A->BC
    B->D
    CD->E
    E->A

无关属性 Extraneous Attributes

  • Attribute A is extraneous（无关的） in α if A ∈ α
    and F logically implies（逻辑蕴含） (F – {α → β}) ∪ {(α – A) → β}.
  • Attribute A is extraneous（无关的） in β if A ∈ β
    and the set of functional dependencies
    (F – {α → β}) ∪ {α →*(*β – A)} logically implies（逻辑蕴含） F.
  • 检查A是无关属性，就要检查能否去掉属性A，需要检查去掉A前后的F函数集合是否等价，就需要检查前后的属性集闭包是否相同

image-20231121130806150

eg. 对第一个集合，要判断A、B是否是无关的

对A就是要求(AB−A)+(AB - A)^+关于F的闭包，即B+(F)={B}B^+(F) = \{B\},没有包含C，故A不是无关属性

对B就是要求(AB−B)+(AB - B)^+关于F的闭包，即A+(F)={A，C}A^+(F) = \{A，C \},包含C，故B是无关属性

也就是要判断哪个元素是否无关，要求去掉这个元素后的式子对集合的闭包是否还包含原式子右边的结果

函数依赖的范式/标准形式 normal form

键属性 - 出现在候选键内的属性

非键属性 - 不出现在任何一个候选键内的属性

第一范式 First Normal Form 1NF

要求所有属性是原子的（不可分割的）

第二范式 Second Normal Form 2NF

若R是1NF，且每个非键属性完全依赖于候选键，则称R为2NF（消除非键属性对候选键的部分依赖）

如果一个关系只是第一范式而不是第二范式，可能会出现数据冗余存储的问题，数据插入可能会缺少键值（插入异常），更新也会同时对多条记录操作（更新异常），还有可能出现删除数据导致重要数据也丢失的问题（删除异常）

如果一个关系的多个候选键都只有一个属性，那么这个关系至少是第二范式

第三范式 Third Normal Form 3NF

若R是2NF，且非键属性不传递依赖于R的候选键（全都是直接依赖），则称R是第三范式

推广，若R是1NF，且所有非键属性既不传递依赖于R的候选键（全都是直接依赖）且全都是全部依赖，则称R是第三范式

如果一个关系中所有属性都是键属性，那它至少是第三范式

如果一个关系只是第二范式而不是第三范式，可能会出现数据冗余存储的问题，数据更新重复多次的异常和删除异常（退学院长就没了）、插入异常（建立新学院缺少学生信息）

但是不能一味的直接暴力拆解总表，需要分解算法

也可以这样判断：要么左边是超键，要么右边是键属性

BC范式 BCNF 增强3NF

如果关系模式R是1NF，且每个属性都不部分依赖于候选键也不传递依赖于候选键，那么称R是BC范式

与3NF的差别就在于，还要求所有键属性也满足：

  • 直接依赖于不包含它自己的候选键
  • 完全依赖于不包含它自己的候选键

所以如果一个3NF只有一个候选键，那么它自然就是BC范式

BC范式自然就是3NF

如果一个关系只是第三范式而不是BC范式，可能会出现数据冗余存储的问题

也可以这样判断：左边全都是超键

多属性依赖集候选键求法

输入：关系模式R及其函数依赖集F

输出：R的所有候选键

方法：

  • 将R的所有属性分为四类：
    • L类：仅出现在F的函数依赖左部的属性；
    • R类：仅出现在F的函数依赖右部的属性；
    • N类：在F的函数依赖左右两边均未出现的属性；
    • LR类：在F的函数依赖左右两边均出现的属性；

​ 并令X代表L、N类，Y代表LR类；

所有的候选键的属性一定会包含的是L类和N类

所有的候选键的属性一定不会包含的是R类 （可以直接去掉）

  • 求X+X^+，若包含了R的所有属性，则X即为R的唯一候选关键字，转（5），否则转（3）；

  • 在Y中取一属性A，求（XA)+（XA)^+,若它包含了R的所有属性,那它就是候选键，则转（4），否则，调换一属性反复进行这一过程，直到试完所有Y中的属性； （3）

  • 如果已找出所有的候选键，则转（5），否则在Y中依此取两个、三个，…，求他们的属性闭包，直到其闭包包含R的所有的属性。 （4）

  • 停止，输出结果。 （5）

eg. 对R = {A,B,C}

去求X+，如果不是候选键继续，如果是候选键，结束并输出

求（XA）+，如果不是候选键继续，如果是候选键，结束并输出

image-20231121145412087

image-20231121145228219

分解 decomposition

把一个表R拆成若干个表Ri，要求R=R1∪R2∪...∪RnR = R_1 \cup R_2 \cup...\cup R_n

lossless-join decomposition 无损连接分解

把所有子表的属性投影后自然连接，与总表的属性投影一致

r = $\Pi_{R_1} ®\Join \Pi_{R_2} ®\Join … \Join \Pi {R_n} ® $

判断是无损连接分解的过程：

将R分解为R1、R2，如果

  • R1 ∩ R2 → R1

或

  • R1 ∩ R2 → R2

eg.

R = (A, B, C)
F = {A → B, B → C)

R1 = (A, B), R2 = (B, C)

由R1 ∩ R2 = {B} and B → BC ，所以是无损连接分解

函数依赖关系保持 Dependency preservation

对子表R1，R2…Rn，各有F1，F2…Fn的函数依赖关系，如果(F1∪F2∪…∪Fn)+=F+(F1 ∪ F2 ∪ … ∪ Fn)^+ = F^+,那么说明总表分解后函数依赖关系保持

$Fi = {X→Y | X→Y∈F^+ ∩ XY⊆Ri } $

Eg. R = (A, B, C), F = {A → B, B → C)

R1 = (A, B), R2 = (B, C)

Dependency preserving

R1 = (A, B), R2 = (A, C)

Not dependency preserving

第三范式分解算法

从第一、二范式分解得到第三范式，同时是无损连接分解与函数依赖关系保持

  • 求F的最小覆盖Fc
  • 对Fc每一个函数依赖关系a→ba\to b,生成关系模式Ri（a,b)，每一次生成的Ri包含的a、b都不能是之前已经生成的R包含过的
  • 如果对每一个Ri，不包括总表F的候选键，那么另外生成新的Rn（候选键的属性）（只选一个候选键生成一个新的Rn即可）

这样生成的关系模式至少是第三范式，且无损连接分解与函数依赖关系保持

BC范式分解算法

根本思想就是将总表不断分解直到全都是BC范式

如果R中有a→ba\to b造成R不是BC范式，那么将R拆成R1（a，b）与R-b

如果R-b中有a′→b′a'\to b'造成R-b不是BC范式，那么将R-b拆成R2（a’，b’）与R-b-b’

…

直到全都是BC范式

无法保证是函数依赖保持，但能保证是无损连接的

数据库设计总体流程

ER图

数据库表

范式识别

分解

反规范化 Denormalization

将高级范式降级为低级范式

高级范式在规范的同时，可能会造成表的数量过多